Hình thang là gì?
Hình thang là một hình học được tạo thành từ hai đường thẳng song song và các cạnh kề của chúng. Hình thang có bốn cạnh và hai cặp cạnh song song. Hình thang có thể có các góc khác nhau, nhưng hai góc đối diện của nó bằng nhau. Đường chéo của hình thang là đường nối hai đỉnh không kề nhau của hình thang. Diện tích của hình thang được tính bằng cách lấy nửa tổng độ dài hai đường chéo và nhân với độ dài đoạn thẳng nối hai đỉnh kề nhau. Hình thang được sử dụng trong nhiều bài toán trong toán học và cũng là một trong những hình học cơ bản.
Tính chất của hình thang
Dưới đây là một số tính chất:
– Có hai đường chéo bằng nhau.
– Hai cặp cạnh đối diện song song với nhau.
– Hai đường chéo của hình thang chia nhỏ hình thang thành hai tam giác bằng nhau.
– Tổng độ dài hai cạnh bên của hình thang bằng tổng độ dài hai cạnh đáy.
– Tổng độ dài hai đường chéo của hình thang bằng tích của độ dài hai cạnh đáy.
– Diện tích của hình thang bằng nửa tổng độ dài hai đường chéo nhân với độ dài đoạn thẳng nối hai đỉnh kề nhau.
Nếu một tam giác và một hình chữ nhật có cùng chiều cao, thì diện tích của hình thang được tạo thành từ chúng là tổng diện tích hai hình.
Những tính chất này giúp ta dễ dàng tính toán và giải quyết các bài toán liên quan đến hình thang trong toán học và các ngành khoa học khác.
Chu vi hình thang
Chu vi bằng tổng độ dài các cạnh của hình thang. Để tính chu vi của hình thang, ta cộng độ dài của hai cạnh đáy và hai cạnh bên lại với nhau. Công thức tính chu vi của hình thang có thể được biểu diễn như sau:
Chu vi = độ dài cạnh đáy 1 + độ dài cạnh đáy 2 + độ dài cạnh bên 1 + độ dài cạnh bên 2
Ví dụ, nếu hình thang có độ dài cạnh đáy 1 là 5cm, độ dài cạnh đáy 2 là 7cm, độ dài cạnh bên 1 là 3cm và độ dài cạnh bên 2 là 4cm, thì chu vi của hình thang đó là:
Chu vi = 5 + 7 + 3 + 4 = 19cm
Do đó, chu vi của hình thang này là 19cm.
Cách tính diện tích hình thang
Công thức tính diện tích của hình thang là:
Diện tích = (độ dài đường chéo 1 + độ dài đường chéo 2) x (độ dài đoạn thẳng nối hai đỉnh kề nhau) / 2
Cụ thể, để tính diện tích, ta cần biết độ dài hai đường chéo và độ dài đoạn thẳng nối hai đỉnh kề nhau. Sau đó, ta áp dụng công thức trên để tính toán diện tích.
Ví dụ, nếu đường chéo 1 của hình thang là 8 cm, đường chéo 2 là 6 cm, và đoạn thẳng nối hai đỉnh kề nhau có độ dài là 10 cm, thì diện tích của hình thang đó là:
Diện tích hình thang = (8 + 6) x 10 / 2 = 70 cm²
Do đó, diện tích của hình thang đó là 70 cm².
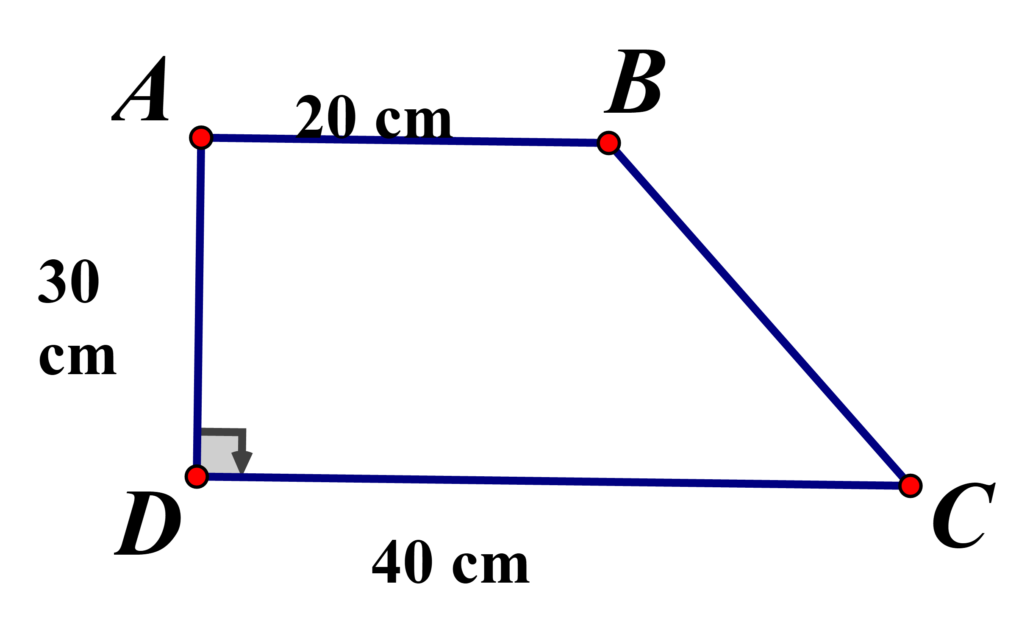
Diện tích hình thang vuông
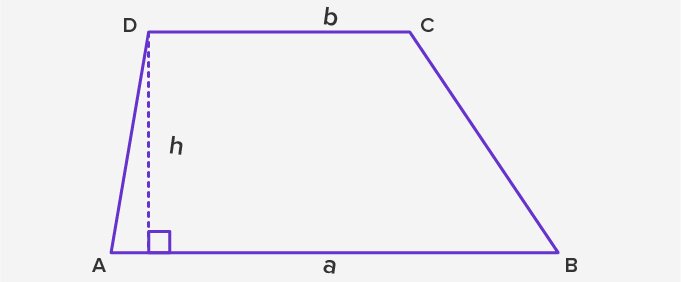
Hình thang vuông là một loại hình thang có một góc vuông. Để tính diện tích, ta sử dụng công thức:
Diện tích hình thang vuông = (độ dài tổng hai cạnh đáy) x (độ dài đường cao) / 2
Trong đó, độ dài đường cao là độ dài đường thẳng kết nối hai đỉnh trên của hình thang vuông.
Ví dụ, giả sử hình thang vuông có độ dài cạnh đáy lớn là 6 cm, cạnh đáy nhỏ là 4 cm và đường cao là 3 cm. Áp dụng công thức tính diện tích hình thang vuông, ta có:
Diện tích hình thang vuông = (6 + 4) x 3 / 2 = 15 cm²
Do đó, diện tích của hình thang vuông là 15 cm².
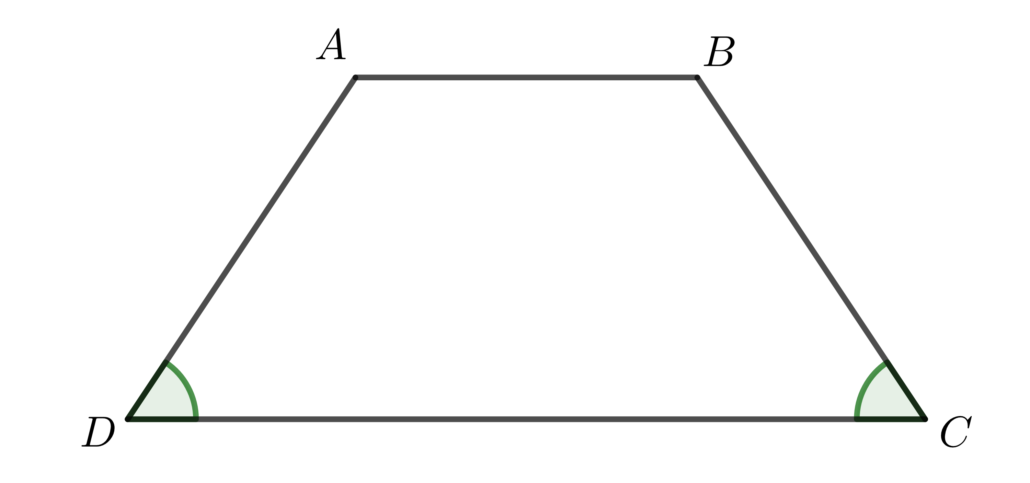
Diện tích hình thang cân
Hình thang cân là một loại hình thang có hai cạnh đáy bằng nhau và hai cạnh bên bằng nhau. Để tính diện tích của hình thang cân, ta sử dụng công thức:
Diện tích hình thang cân = (độ dài tổng hai cạnh đáy) x (độ dài đường cao) / 2
Trong đó, độ dài đường cao là độ dài đường thẳng kết nối hai đỉnh trên của hình thang cân.
Nếu đặt độ dài đáy của hình thang là b, độ dài cạnh bên là a và độ dài đường cao từ đỉnh của một đáy đến đường đối diện là h, ta có thể sử dụng công thức:
Diện tích hình thang cân = (a + b) x h / 2
Ví dụ, giả sử hình thang cân có đáy bằng 6 cm, cạnh bên bằng 4 cm và đường cao bằng 3 cm. Áp dụng công thức tính diện tích hình thang cân, ta có:
Diện tích hình thang cân = (4 + 6) x 3 / 2 = 15 cm²
Do đó, diện tích của hình thang cân đó là 15 cm².
Công thức tính chiều cao hình thang
Để tính chiều cao của hình thang, ta có thể sử dụng công thức sau:
Chiều cao = diện tích / độ dài đáy đối diện
Trong đó, diện tích là diện tích của hình thang, độ dài đáy đối diện là độ dài đoạn thẳng nối hai đỉnh không kề nhau của hình thang.
Nếu đặt độ dài đáy lớn của hình thang là b, độ dài đáy nhỏ là a và độ dài đường cao là h, ta có thể sử dụng công thức:
Chiều cao = (a + b) x h / (2 x độ dài đoạn thẳng nối hai đỉnh không kề nhau)
Ví dụ, giả sử hình thang có đáy lớn bằng 8 cm, đáy nhỏ bằng 4 cm và độ dài đoạn thẳng nối hai đỉnh không kề nhau bằng 6 cm. Nếu diện tích của hình thang là 24 cm², ta có thể tính được chiều cao của hình thang đó:
Chiều cao = 24 / 6 = 4 cm
Do đó, chiều cao của hình thang đó là 4 cm.
Ứng dụng của hình thang trong cuộc sống
Hình thang là một khái niệm hình học phổ biến và được ứng dụng trong nhiều lĩnh vực trong cuộc sống. Sau đây là một số ví dụ về ứng dụng của hình thang:
– Kiến trúc và xây dựng: Hình thang được sử dụng trong thiết kế và xây dựng các công trình kiến trúc như các cửa sổ, cửa ra vào, các tấm chắn trang trí, các đồ vật trang trí nội thất.
– Máy móc và kỹ thuật: Hình thang được sử dụng để thiết kế các bộ phận của các máy móc và kỹ thuật khác nhau như các bánh răng hình thang, các bộ phận chuyển động hình thang, các bộ phận kết nối và truyền động hình thang.
– Giải toán và học tập: Hình thang được sử dụng trong giải toán hình học, học tập toán học ở các trường học và các trung tâm giáo dục. Các bài toán liên quan đến hình thang giúp học sinh hiểu rõ hơn về các tính chất hình học cơ bản và các công thức tính toán.
– Nghệ thuật: Hình thang cũng được sử dụng trong nghệ thuật, trong các bức tranh, hình ảnh trang trí, vải may, hoa văn trang trí…
– Kinh doanh: Hình thang cũng được ứng dụng trong kinh doanh, đặc biệt là trong lĩnh vực đo lường và tính toán diện tích của các khu đất, tài sản bất động sản.
Vì vậy, hình thang là một khái niệm hình học quan trọng và được ứng dụng rộng rãi trong cuộc sống.

