Tam giác nhọn là gì? Cách vẽ tam giác nhọn

Hình tam giác là gì?

Tam giác nhọn là một loại tam giác mà tất cả ba góc trong của nó đều nhỏ hơn 90 độ. Cụ thể, các góc trong của tam giác nhọn có độ lớn nhỏ hơn 90 độ, không có góc nào bằng hoặc lớn hơn 90 độ. Điều này làm cho tam giác có dạng hơi “spiky” (nhọn), không có góc tròn hoặc bẹt.

Tính chất

– Tất cả ba góc trong của tam giác nhọn đều nhỏ hơn 90 độ. Điều này có nghĩa là không có góc nào trong tam giác đó bằng hoặc lớn hơn 90 độ.

– Tổng của ba góc trong của tam giác nhọn luôn bằng 180 độ. Đây là một định lý cơ bản trong hình học được gọi là định lý tổng ba góc trong của tam giác.

– Trong tam giác nhọn, độ dài của mỗi cạnh phải lớn hơn hiệu độ dài của hai cạnh kia và nhỏ hơn tổng độ dài của chúng. Điều này được gọi là bất đẳng thức tam giác và là một điều kiện cần để có thể tạo thành một tam giác.

– Cạnh đối diện với góc lớn hơn sẽ có độ dài lớn hơn. Ngược lại, góc đối diện với cạnh lớn hơn sẽ có độ lớn lớn hơn. Điều này thể hiện mối quan hệ giữa các thành phần trong tam giác nhọn.

– Định lý cosin và định lý sin là các công thức quan trọng trong tính toán các độ dài và góc của tam giác nhọn.

– Tam giác nhọn có một trung tâm duy nhất là trọng tâm. Trọng tâm là điểm trọng tâm của các đường trung tuyến của tam giác và có nhiều tính chất đặc biệt trong hình học.

Tam giác nhọn nội tiếp đường tròn

Tam giác nhọn nội tiếp đường tròn là một tam giác mà mọi đỉnh của nó đều nằm trên đường tròn nội tiếp của tam giác đó.

tam giac nhon abc noi tiep duong tron — *Tam giác nhọn nội tiếp đường tròn*

Tam giác nhọn ngoại tiếp đường tròn

Tam giác ngọn ngoại tiếp đường tròn là một loại tam giác mà tất cả các đỉnh của nó đều nằm trên đường tròn ngoại tiếp tam giác. Cụ thể, đường tròn ngoại tiếp này đi qua đồng thời cả ba đỉnh của tam giác. Điều này có nghĩa là tất cả các đoạn thẳng nối từ tâm của đường tròn ngoại tiếp đến các đỉnh của tam giác đều có cùng độ dài, tức là bán kính của đường tròn ngoại tiếp tam giác là bằng nhau.

tam giac nhon abc ngoai tiep duong tron — *Tam giác ngọn ngoại tiếp đường tròn*

Đường thẳng Euler

Đường thẳng Euler là một đường thẳng đặc biệt trong tam giác, nó được hình thành bằng cách nối các điểm đặc biệt trong tam giác như trực tâm, trọng tâm, và tâm của đường tròn ngoại tiếp tam giác.

Cách vẽ tam giác nhọn abc

Để vẽ tam giác thường đơn giản nhất, trước tiên bạn lấy 3 điểm bất kỳ trên giấy, sau đó lấy thước kẻ nối các điểm với nhau, vậy là ta đã có một hình tam giác bất kỳ. Trường hợp muốn vẽ hình tam giác khi biết số đo các cạnh ta thực hiện như sau:

cach ve tam giac nhon — *Cách vẽ tam giác nhọn abc*

Ví dụ: Vẽ tam giác ABC biết BC = 6cm, AB = 2cm; AC = 5cm. Ta thực hiện lần lượt các bước dưới đây:
Trước tiên, ta vẽ đoạn thẳng BC = 6cm, sau đó vẽ cung tròn tâm B bán kính bằng 2cm và vẽ cung tròn tâm C bán kính bằng 5cm.
Ta được giao điểm của hai cung tròn gọi là điểm A. Ta nổi các đoạn thẳng AB; AC, như vậy ta có được tam giác ABC theo yêu cầu đề bài đã đặt ra.

Công thức tính diện tích tam giác nhọn

Tính diện tích tam giác bằng hình học

Diện tích S bằng ½bh, trong đó b là độ dài của một cạnh bất kỳ của tam giác (thường gọi là đáy) và h là độ dài đường cao hạ từ đỉnh đối diện xuống cạnh ấy.

Từ một tam giác (màu xanh lục), ta sẽ sao một tam giác bằng nó,(màu xanh lam), quay góc 180°, và ghép chúng thành hình bình hành. Cắt một phần của hình bình hành, ghép lại thành hình chữ nhật. Vì diện tích hình chữ nhật là bh, nên diện tích tam giác là ½bh.

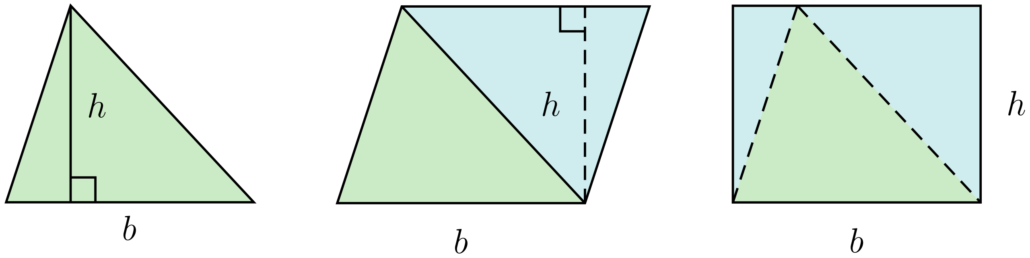
dien tich tam giac ngon bang hinh hoc — *Diện tích tam giác bằng hình học*

Nói cách khác, diện tích tam giác bằng độ dài cạnh đáy nhân với chiều cao chia 2: $S={\frac {1}{2}}bh$ Đặc biệtTam giác vuông thì diện tích sẽ tính là một nửa tích hai cạnh góc vuông hoặc nửa tích đường cao với cạnh huyền.Tam giác đều thì diện tích sẽ tính là bình phương 1 cạnh nhân với ${\frac {\sqrt {3}}{4}}$ .

Tính diện tích tam giác nhọn bằng vectơ

Nếu tứ giác ABDC là hình bình hành thì diện tích của nó được tính bởi công thức:

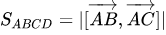
trong đó $[{\overrightarrow {AB}},{\overrightarrow {AC}}]$ là tích có hướng của hai vectơ ${\overrightarrow {AB}}$ và ${\overrightarrow {AC}}$ .

Diện tích tam giác ABC bằng một nửa diện tích của hình bình hành ABDC nên:

Tính diện tích tam giác nhọn bằng lượng giác

tinh dien tich tam giac nhon bang luong giac

Vì $h=a.\sin \gamma \,$ và $S={\frac {1}{2}}.b.h$ nên ta có:

sin⁡ $S={\frac {1}{2}}.a.b.\sin \gamma$

Một số bài tập áp dụng tính diện tích hình tam giác nhọn

Bài tập 1: Tính diện tích của hình tam giác nhọn biết:
a. Độ dài của đáy là 16 m, chiều cao 13 cm.
b. Độ dài đáy 8 cm và chều cao 5 cm.

Lời giải:
a. Áp dụng công thức tính diện tích của tam giác thường ta có diện tích của hình tam giác là:
(16 x 13):2 = 104 (cm2).
b. Diện tích cua hình tam giác là:
(8 x 5):2 = 20 (cm2).

Bài tập 2: Tính diện tích của tam giác vuông với
a. Hai cạnh của góc vuông lần lượt là 6 cm và 8 cm.
b. Hai cạnh của góc vuông lần lượt là 12 cm và 18 cm.

Lời giải:
a. Diện tích của tam giác là: (6 x 8):2 = 24 (cm2)
b. Diện tích của tam giác là: (12 x 18):2 = 108 (cm2).

Bài tập 3: Hãy tính diện tích của tam giác cân có
a. Độ dài của cạnh đáy bằng 15 cm và đường cao là 13 cm.
b. Độ dài của cạnh đáy bằng 51 m và đường cao là 32 m.

Lời giải:
a. Diện tích của tam giác bằng: (15 x 13):2 = 97,5 (cm2)
b. Diện tích của tam giác là: (51 x 32) : 2 = 816 (m2).

Xem thêm: Hình bát giác là gì?

Ví dụ cho tam giác nhọn abc tính chu vi tam giác

Ví dụ 1:
A = (2, 3), B = (5, 7), C = (9, 1)

Để tính độ dài các cạnh, ta sử dụng công thức tính khoảng cách giữa hai điểm trong hệ tọa độ Descartes:
AB = √[(5 – 2)² + (7 – 3)²] = √(3² + 4²) = 5
AC = √[(9 – 2)² + (1 – 3)²] = √(7² + 2²) ≈ 7.28
BC = √[(9 – 5)² + (1 – 7)²] = √(4² + 6²) ≈ 7.21
Vậy chu vi tam giác ABC là AB + AC + BC = 5 + 7.28 + 7.21 ≈ 19.49

Ví dụ 2:
A = (1, 2), B = (4, 3), C = (3, 5)

AB = √[(4 – 1)² + (3 – 2)²] = √(3² + 1²) ≈ 3.16
AC = √[(3 – 1)² + (5 – 2)²] = √(2² + 3²) ≈ 3.61
BC = √[(3 – 4)² + (5 – 3)²] = √(1² + 2²) ≈ 2.24
Vậy chu vi tam giác ABC là AB + AC + BC = 3.16 + 3.61 + 2.24 ≈ 9.01

Ví dụ 3:
A = (-1, -2), B = (2, -1), C = (0, 3)

AB = √[(2 – (-1))² + (-1 – (-2))²] = √(3² + 1²) ≈ 3.16
AC = √[(0 – (-1))² + (3 – (-2))²] = √(1² + 5²) ≈ 5.10
BC = √[(0 – 2)² + (3 – (-1))²] = √(2² + 4²) ≈ 4.47
Vậy chu vi tam giác ABC là AB + AC + BC = 3.16 + 5.10 + 4.47 ≈ 12.73

Cho tam giác nhọn ABC nội tiếp đường tròn (O), Các đường cao BD , CE ( D thuộc AC , E thuộc AB ) của tam giác kéo dài lần lượt cắt đường tròn (O) tại các điểm M và N ( M khác B , N khác C ). Chứng minh tứ giác BCDE nộit tiếp được trong 1 đường tròn.

Một tam giác nhọn được gọi là tam giác nội tiếp đường tròn nếu ba đỉnh của tam giác đều nằm trên một đường tròn. Điều này có nghĩa là đường tròn này tiếp xúc với đoạn thẳng nối giữa các đỉnh của tam giác ở các điểm trên đường tròn.
Trong một tam giác nội tiếp đường tròn, các đường cao, trung tuyến, đường phân giác, đường trung trực đều đi qua tâm đường tròn ngoại tiếp tam giác đó. Đồng thời, mỗi góc của tam giác bằng nửa tổng của hai góc ở tâm của hai cung tương ứng trên đường tròn.
Các tính chất của tam giác nội tiếp đường tròn là rất quan trọng trong hình học Euclid, đặc biệt là trong các vấn đề liên quan đến tính toán đường tròn và tam giác.

Để chứng minh tứ giác BCDE nội tiếp trong đường tròn, ta cần chứng minh góc BCE = góc BDE.

Ta có:

Góc BCE = góc BCO (vì BC là đường cao nên góc BCE là góc giữa BC và đường tròn ngoại tiếp tam giác ABC tại O, do đó góc BCE bằng góc ở tâm tương ứng trên đường tròn ngoại tiếp tam giác ABC).

Góc BDE = góc BMN (vì BD là đường cao nên góc BDE là góc giữa BD và đường tròn (O) tại N, do đó góc BDE bằng góc BMN ở tâm tương ứng trên đường tròn (O)).
Vì BMNC là tứ giác nội tiếp (do M và N đều nằm trên đường tròn (O)), nên ta có:
góc BMN + góc BCN = 180 độ (do đây là góc ở tâm chắn cùng một cung MN, BC)
Tương tự, ta cũng có:
góc CNM + góc CBM = 180 độ (do đây là góc ở tâm chắn cùng một cung MN, CB)
Tổng hai phương trình trên ta được:
góc BMN + góc CNM + góc BCN + góc CBM = 360 độ
Vì góc BMN = góc BDE và góc BCN = góc BCE, nên ta có:
góc BDE + góc BCE + góc CBM + góc CNM = 360 độ

Tức là tứ giác BCDE nội tiếp trong đường tròn với góc BCE = góc BDE. Do đó, ta đã chứng minh được điều cần chứng minh.

Ứng dụng của Tam Giác Nhọn Trong Ngành Bao Bì Nhựa

Trong lĩnh vực sản xuất bao bì nhựa, hình học đóng vai trò quan trọng trong thiết kế, tối ưu kết cấu và nâng cao tính thẩm mỹ của sản phẩm. Trong đó, tam giác nhọn là một trong những hình học được ứng dụng rộng rãi nhất nhờ khả năng phân bổ lực tốt, tạo điểm tựa chắc chắn và nâng cao độ bền của bao bì.

Bài viết dưới đây sẽ phân tích chi tiết ứng dụng của tam giác nhọn trong ngành bao bì nhựa, đặc biệt trong các sản phẩm mà SPK Packaging đang cung cấp như: hang tabs, hộp nhựa trong suốt, hộp nhựa tròn, tấm nhựa trong,…

Tam giác nhọn là gì? Vì sao quan trọng trong thiết kế bao bì?

Tam giác nhọn là tam giác có ba góc đều nhỏ hơn 90°. Đây là dạng tam giác có tính ổn định cao, khả năng phân tán lực tốt và thường được dùng trong kiến trúc, xây dựng cũng như cơ khí.

Trong ngành bao bì nhựa, tam giác nhọn được xem là một khối hình học tối ưu để tạo kết cấu vững, giúp giảm độ cong vênh, tăng khả năng chịu lực và ổn định khi đóng gói, trưng bày hoặc vận chuyển.

Ưu điểm của tam giác nhọn khi ứng dụng vào thiết kế bao bì:

Phân bổ lực tốt, chống biến dạng.

Tạo các điểm chịu lực hiệu quả.

Tăng cứng trong những vị trí cần thiết.

Hỗ trợ tạo hình thẩm mỹ, tinh gọn.

Tối ưu không gian đóng gói.

Ứng dụng của tam giác nhọn trong ngành bao bì nhựa

2.1. Tăng độ cứng vững cho các sản phẩm hang tab

Trong các sản phẩm Hang Tabs – phụ kiện treo hàng phổ biến trong ngành bán lẻ – kết cấu gia cường thường sử dụng các đường gân dạng tam giác nhọn.

Nhờ hình dạng thuôn cong và góc nhọn, các đường gân này:

Chịu lực treo tốt hơn.

Không dễ rách tại các điểm chịu tải.

Giảm cong vênh của bề mặt treo.

👉 Xem dòng sản phẩm: Hang Tabs SPK Packaging

2.2. Tạo cấu trúc tăng cứng cho hộp nhựa trong suốt

Nhiều loại hộp nhựa trong suốt được thiết kế các cạnh bo nhọn hoặc gân tăng cứng dạng tam giác nhọn để:

Giữ form hộp tốt hơn.

Chống móp méo khi xếp chồng hoặc vận chuyển.

Tối ưu sự trong suốt mà không làm giảm độ bền.

Tam giác nhọn giúp phân bổ lực vào các vị trí hợp lý, hạn chế tác động trực tiếp lên bề mặt hộp.

👉 Tham khảo mẫu: Hộp nhựa trong suốt SPK

2.3. Ứng dụng trong cấu trúc nắp và thân hộp nhựa tròn

Ngay cả các hộp nhựa tròn, vốn có dạng hình học mềm mại, cũng thường sử dụng tam giác nhọn trong:

Gân cài khóa nắp.

Đường bo cứng dưới đáy hộp.

Cấu trúc lồng ghép giúp xếp chồng không bị trượt.

Gân tam giác nhọn giúp cố định nắp chắc chắn, đồng thời tăng độ ổn định khi đặt hộp trên bề mặt.

👉 Xem thêm: Hộp nhựa tròn SPK

2.4. Tăng độ bền cho các tấm nhựa trong

Trong tấm nhựa trong, tam giác nhọn được ứng dụng trong các dạng:

Gân chống cong.

Lỗ treo tam giác nhọn.

Góc nhọn bo chạy viền giúp tăng lực chịu uốn.

Thiết kế này giúp tấm nhựa:

Cứng hơn.

Giữ bề mặt phẳng lâu dài.

Không bị vênh khi thay đổi nhiệt độ.

👉 Sản phẩm: Tấm nhựa trong SPK Packaging

Tam giác nhọn và vai trò trong tối ưu hóa không gian bao bì

Không chỉ tăng cứng, tam giác nhọn còn giúp:

Tối ưu diện tích sử dụng: dễ bố trí trong các kết cấu hộp, khay.

Tiết kiệm nguyên vật liệu: giảm độ dày mà vẫn giữ độ bền.

Tạo điểm nhấn thẩm mỹ: cạnh nhọn mang lại cảm giác tinh tế, hiện đại.

Nhờ ưu điểm này, tam giác nhọn trở thành một lựa chọn phổ biến trong thiết kế bao bì nhựa cao cấp.

SPK Packaging – chuyên gia trong thiết kế bao bì theo tiêu chuẩn hình học tối ưu

Với:

Nhà máy tại Bình Dương

Văn phòng tại TP.HCM

Hệ thống sản phẩm đa dạng

Đội ngũ thiết kế am hiểu kết cấu hình học

SPK Packaging ứng dụng linh hoạt các dạng hình tam giác nhọn vào thiết kế nhằm nâng cao độ bền, tính thẩm mỹ và tối ưu chi phí sản xuất cho khách hàng.

Kết luận

Tam giác nhọn là một hình học có giá trị ứng dụng cao trong ngành bao bì nhựa. Từ tăng độ cứng cho hang tabs, hộp nhựa đến tối ưu cấu trúc tấm nhựa, tam giác nhọn giúp sản phẩm bền hơn, ổn định hơn và đẹp hơn.

Nếu bạn đang tìm kiếm giải pháp bao bì nhựa chất lượng cao, hãy liên hệ SPK Packaging để được tư vấn và lựa chọn sản phẩm phù hợp nhất.